FISICA-MATEMATICA I

INTRODUÇÃO

Inicialmente faremos um breve estudo sobre as circunstâncias que levaram à criação do cálculo infinitesimal e da ciência moderna. Tal estudo é imprescindível para uma boa compreensão da pesquisa científica atual. O restante do artigo desenvolve conceitos e questionamentos pertinentes aos processos infinitesimais.

Quando na Grécia Antiga se deu a descoberta dos incomensuráveis por Pitágoras, além da ruína total de sua escola, ocorreu uma grande reviravolta na ordenação matemática do Cosmo ou no modelo do mundo dos gregos. Buscando uma nova compreensão desse mundo, então, Parmênides distinguia aquilo que era objeto puramente da razão – o que chamou de verdade– e o que era dado pela observação, pelos sentidos – o que denominou de opinião. Opondo, assim, a razão à opinião, Parmênides abriu um debate de uma importância e alcance excepcionais, o qual, ainda hoje, tem gerado muita controvérsia no meio científico: as relações entre razão e a experiência, entre a teoria e a prática, entre o idealismo e o materialismo.

Ao existente Parmênides reconhecia como verdadeiras as seguintes características: unidade, homogeneidade, continuidade, imobilidade, eternidade; relega, então, para o vulgo da opinião, todos os outros atributos que porventura sejam contrários àqueles. Foi a partir das concepções de Parmênides e do fenômeno da incomensurabilidade, que Zenão de Eléia constatou, através da razão, a impossibilidade do movimento: a incomensurabilidade implicando o infinito, paradoxalmente, implicava também a imobilidade, o não movimento. Porém, Heráclito, contemporâneo de Parmênides, afirmava embasado na opinião, que tudo no mundo é movimento, nada permanece imóvel, tudo muda, se transmuta. Abaixo, temos as provas usadas por Zenão contra os pitagóricos e contra Heráclito:

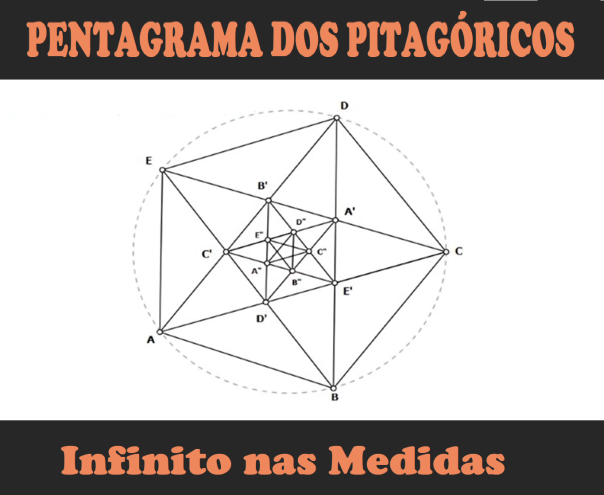
Demonstração geométrica da Incomensurabilidade

Traçando as diagonais de um pentágono regular obtemos um pentagrama… no interior deste  podemos construir outro pentágono, o qual, traçando  também suas diagonais, obtemos mais um pentagrama… e assim sucessivamente de modo que a figura é sem fim em seu interior.

Mas podemos  medir um lado do pentágono, seja de DE, pela diagonal AC simetricamente oposta; neste caso o quadrilátero ED’CD é um paralelogramo e portanto CD’ = DE. Portanto, o lado DE ou CD’ está contido uma vez na diagonal CA, ficando o resto AD’. Quando se mede AD’ em AE’ (que é igual ao lado DE da mesma forma) está aí contida uma vez deixando o resto E’D’. Ora, E’D’ é o lado do pentágono interno A’B’C’D’E’ e a diagonal deste C’A’ é igual a D’A (pois AD’A’C” é um paralelogramo. Depois a mesma relação se repete e o processo da ‘diminuição recíproca” continua sem fim.

Este interessante resultado chamou a atenção de Zenão que pôs fim ao domínio da Escola de Pitágoras!!!

Paradoxo de Zenão – Aquiles e a Tartaruga

Se a tartaruga começa a corrida com certa vantagem sobre Aquiles, quando este alcançar a sua posição inicial Po, a tartaruga já se terá movido para a posição P1, por muito próxima que seja. Quando Aquiles chegar a P1, a tartaruga já estará em P2, e asim sucessivamente, pelo que parece que Aquiles nunca conseguirá alcançar a tartaruga. Contudo, se supusermos que Aquiles corre dez vezes mais depressa que a tartaruga e que demora um segundo a chegar a Po, precisaria de uma décima para chegar a P1, uma centésima para chegar a P2,…, mas,

                         

Pelo que em 1 segundo e 1/9 conseguirá alcançá-la. Num segundo e duas décimas tê-la-á ultrapassado. A intuição dos gregos fracassou ao julgar que uma soma de termos infinitos positivos há de dar necessariamente infinita!!!

Atrelados ainda à concepção materialista do Cosmo, os esquemas de Parmênides e de Heráclito não conseguiram explicar o sensível porque buscavam tal explicação também através do sensível… Isto provocou grande perplexidade entre os gregos no que diz respeito à concepção do Universo.

Mas chega então Platão que, enfrentando o problema da realidade e das aparências, da unidade ou pluralidade do ser, e partindo da teoria do Eleata, conseguiu dar novo rumo à questão da inteligibilidade do Universo através da descoberta da imaterialidade, do imaterial, do supra-sensível; reconheceu, então, a existência de dois planos do ser: um, fenomênico e visível; outro, invisível e metafenomênico, captável apenas com a mente e, por conseguinte, puramente inteligível.

Com isso, com a distinção entre esses dois planos, o sensível e o inteligível, parecia superada, “definitivamente”, a antítese entre Parmênides e Heráclito;  ou seja,   a  verdadeira  causa que explica tudo não é algo sensível, mas inteligível. Platão denominou estas causas de natureza não física, essas realidades inteligíveis, usando o termo Ideia que significa forma. Tinha fim, assim, a grande preocupação de Platão, o objetivo final de sua filosofia, pois havia obtido uma coisa que guardava identidade permanente e à qual o pensamento pudesse se prender: se a realidade sensível é fluente e, portanto, o contrário do permanentemente idêntico, voltemos-lhe as costas e refugiemo-nos do lado das Idéias.

Contudo, afirmando serem as coisas sensíveis nada mais que imagens ou cópias das formas, das idéias, a verdade não se poderia adquirir pelo exame do universo exterior sensível, por meio dos sentidos, mas apenas pelo pensamento puro, pela atividade da alma, isolada do corpo; aliás, este, não faz mais do que perturba-la, impedindo-a de pensar.

A ciência e a filosofia gregas, lendo na cartilha de Platão, impuseram-se, então, a partir do dobrar do século V para IV a.C., duas limitações: rejeição do devir como base duma explicação racional do mundo; e rejeição do manual e do mecânico para fora do domínio da cultura. Estas duas limitações, portanto, vão pesar duramente sobre as possibilidades de uma construção científica do Cosmo pelos povos gregos, pois, além da MATEMÁTICA que, banindo o infinito de seus estudos, impossibilitou o tratamento matemático de sistemas dinâmicos, do movimento, a FÍSICA, também, eleminando a experiência sensível de sua metodologia, como algo sem nenhum valor, tornou impossível o tratamento objetivo e de precisão do devir, do real (é bom frisar que ao devir está relacionado o infinito e, ao mecânico, a experiência). Ainda, a MATEMÁTICA passou a ser toda geometrizada; ou seja, a aritimética foi desprestigiada e passou a imperar a Teoria das Proporções de Eudoxo: exemplo maior disto são Os Elementos de Euclides.

           

A abominação dos gregos pelo INFINITO, portanto, fez a ciência grega recuar: não era possível aos helenos tratar racionalmente ou matematicamente o MOVIMENTO. Somente depois de quase dois mil anos – após a grande unificação da análise com a geometria, propiciada pelo conceito de função -, Newton e Leibniz, criando o CÁLCULO INFINITESIMAL, torna a ciência capacitada para tratar com o movimento: o infinito deixa de ser um monstro e seu estudo propicia todo o desenvolvimento ulterior da humanidade. Devemos também citar a ARITMETIZAÇÃO que se deu na matemática, já nos dias modernos, realizada pelos grandes matemáticos Weierstrass e Dedekind.

Mas, havia agora a grande disputa entre realistas e racionalistas (empiristas e racionalistas) – iniciada após a distinção entre os planos do sensível e do inteligível, por Platão, e a distinção entre razão e opinião, por Parmênedes: ou seja, entre aqueles que julgam ser, o conhecimento, somente dado pela opinião e aqueles que julgam ser, o conhecimento, somente dado pela razão, respectivamente. Galileu, por fim, resolveu a questão criando um novo método de pesquisa, o Método Científico, para a construção de modelos dos fenômenos físicos. Utilizando a metodologia científica, o pesquisador, se colocando dialeticamente entre o realismo e o racionalismo, entre a experiência e a teoria, elege a NATUREZA como única capaz de ajuizar qualquer discussão sobre a VERDADE!!!

Hoje, Pitágoras, Heráclitoe Galileu são festejados por toda a comunidade científica internacional, pois, o Pitagorismo, relação entre coisa e número, está presente em todo o conhecimento científico, a Natureza dá provas a todo momento de sua evolução constante, e o Método Científico é o responsável por todo o progresso tecnológico do mundo hodierno.  

NATUREZA DO CÁLCULO INFINITESIMAL

Ocorrendo que uma variável y seja função de outra variável x, o CI se propõe a estudar essa dependência em dois momentos. Inicialmente descobre-se uma representação analítica y = f( x ) expresando essa dependência, a seguir estuda-se as propriedades dessa função .

 

1.           Problema da identificação: Barrow

Desejo descobrir a função f que expressa a dependência y = f( x ) entre x e y. A experiência mostra que, normalmente, é difícil de conseguirmos fazer isso diretamente. Assim sendo, o CI usa uma abordagem indireta em duas etapas:

o Etapa diferencial: Descobre-se relação entre a variação infinitesimal dx de x e a variação infinitesimal dy de y.

o     Etapa integral: obtém-se a expressão analítica de y = f( x ) a partir da relação entre dy e dx.

O sucesso dessa estratégia depende dos seguintes fatos:

o    como dx e dy são versões infinitesimais de x e y, na busca da expressão de dy em termos de dx podemos desprezar infinitésimos de ordem superior

o   a existência de uma regra, descoberta por Barrow e chamada de Teorema Fundamental do Cálculo Integral, que permite-nos passar de dy/dx para y = y( x ).

 

2.           Problema da elucidação: Fermat

As propriedades locais de y = y( x ) podem ser descobertas estudando o que ocorre com y ao x variar infinitesimalmente. Com efeito, por exemplo, Fermat mostrou que nos pontos de máximo ou mínimo de y = y( x ) as variações dx produzem uma dy=0; consequentemente, esses pontos podem ser determinados através da resolução da equação dy/dx = 0. Equação essa que é muito fácil de obtermos.

A exploração  da  interpretação  geométrica  da  taxa dy/dx permite o estudo de muitas outras  propriedades locais de    y = y( x ):  crescimento, convexidade, etc bem como a obtenção de aproximações locais.

E quanto as propriedades globais de y = y( x ), tais como valor médio de y ao longo de um intervalo de variação de x?
Para isso, o CI da preferência ao uso da chamada integral de y = y( x ), a qual é o resultado do acúmulo ou soma das parcelas infinitesimais y( x ) dx ao longo de um intervalo de variação de x. Essa noção de acúmulo de infinitesimais é extremamente fértil, tanto em aplicações estritamente matemáticas ( áreas, volumes, valores médios, etc ) como físicas ( trabalho, pressão, etc).

Fontepesquisa:(CARAÇA, BENTO J., 1951, Conceitos fundamentais da Matemática, Lisboa; http://euler.mat.ufrgs.br/~portosil/oque.html)

POSTED BY SELETINOF 10:40 PM   

FISICA-MATEMATICA II

POR QUE INFINITESIMAL?

1.           pois usa o formalismo infinitesimal esboçado acima e que remonta aos primeiros mestres dessa arte: Kepler, Cavalieri, Fermat, Newton, Leibniz, os Bernoullis, Taylor, Mac Laurin, Euler e tantos outros.

2.           preferimo-lo, em oposição ao enfoque mais recente de Cauchy-Weierstrass e que substitui o uso dos infinitésimos por desigualdades tipo epsilon-delta, por ser mais natural e intuitivo, alem de corresponder muito melhor ao modo de pensar dos físicos e engenheiros.

                        

QUAL A ORIGEM DO CÁLCULO INFINITESIMAL?

 

1.           A motivação de tudo

Com a divulgação dos escritos matemáticos de Archimedes na Europa, em várias edições impressas c. 1550, é retomado com enorme ímpeto o estudo dos métodos infinitesimais. De início, a preocupação é apenas a de continuar a tradição arquimediana aplicando seus métodos na determinação de áreas, volumes e centros de gravidade: Comandino, Maurolico, Luca de Valerio e Stevin (1570-1585) são os primeiros nomes que se destacam.

Mas logo o espírito renascentista se faz notar através de Galileo c.1620 . Esse, ao contrário dos já citados, procurou ir além dos gregos e não mais limitar-se a estudar as grandezas de natureza geométrica da Astronomia, Óptica e Estática. Ele é a primeira grande inteligência a estudar quantitativamente áreas nunca abordadas pelos gregos clássicos: Cinemática, Dinâmica, Elasticidade, etc.

O enorme prestígio de Galileo possibilitou que todos vissem que os métodos infinitesimais eram os instrumentos adequados para o estudo dessas novas disciplinas. Os 50 anos seguintes são dedicados tanto ao aperfeiçoamento desses métodos (por discípulos de Galileo e muitos outros matemáticos italianos, franceses e ingleses) como na sua aplicação ao desenvolvimento das áreas citadas acima e da Mecânica dos Fluídos.

Assim, quando já eram passados 100 anos desde Comandino, Maurolico e etc e surgiu Newton, esse já encontrou uma ampla base matemática e física para a composição do primeiro grande monumento celebrando o poder do Cálculo Infinitesimal: o Philosophiae Naturalis Principia Mathematica, publicado em 1687 e com o qual Newton conseguia unificar a Mecânica do Céu e a da Terra.

                

As gerações de matemáticos que vieram após Newton em grande maioria seguiram seus passos, procurando novos resultados tanto nos aspectos técnicos do Cálculo como em suas aplicações a aspectos teóricos da Mecânica. Mas , já no sec 1700, apareceram oportunidades para um uso mais prático do Cálculo na análise estática, dinâmica e termodinâmica das máquinas industriais, das quais a cada dia eram solicitadas maior potência e velocidade. Tudo passou a ser objeto de cálculo e análise: da forma adequada dos dentes das engrenagens à melhoria da eficiência das máquinas a vapor.

De lá para cá o CI não cessou de se desenvolver teoricamente e de ter novas aplicações, sendo hoje um instrumento matemático absolutamente imprescindível para todo cientista e engenheiro.

 

2.    A construção dos alicerces do Cálculo Infinitesimal 

 

o        A Álgebra Literal

A notação algébrica é um excelente veículo para produzirmos e expressarmos os resultados do CI. Com efeito, hoje é até difícil imaginarmos a existência do CI sem a notação algébrica. Contudo, é uma das grandes coincidências da História da Matemática que o surgimento do CI tenha sido contemporâneo à introdução da notação literal em Álgebra.

                

Sempre é uma grande surpresa, para quem se inicia no estudo da História da Matemática, saber que a arte da resolução das equações (o que hoje chamamos de Álgebra Clássica) por dezenas de séculos adotou o método e notação geométrica para resolver seus problemas. Com efeito, foi só em c. 1600 que Viète introduziu a Logistica Speciosa, ie o cálculo literal.

Isso não foi feito pequeno, pois além de ter de romper com o quase sagrado paradigma grego que centrava toda a Matemática em torno da Geometria Euclidiana:

§     foi preciso um estudo exaustivo das regras de operação dos novos símbolos, o que foi feito por Viète, Descartes e seus seguidores 1590-1650.

§  foi preciso mostrar que as manipulações algébricas tinham o mesmo status lógico que os argumentos geométricos. Ou seja, que podíamos representar uma equação literalmente e, através de regras apropriadas, transformá-la sucessivamente até obter as características desejadas da incógnita.

§     foi também percebido que essa notação permitia fazer úteis generalizações como:

1 + 2 + 3 + … + n = n (n+1) / 2

1² + 2² + 3² + … + n² = n (n+1) (2n+1) / 6

com as quais ficava fácil achar áreas pela versão grega do Cálculo Integral, ie pelo método da exaustão.

o        Fermat

o        Método dos Indivisíveis de Cavalieri

o        Os Teoremas Fundamentais do Cálculo, de Barrow

 

3.   Mas então não é verdade que Newton e Leibniz inventaram o CI

                    

o  Certamente não, pois que quando Newton e Leibniz começaram a trabalhar já tinham sido estabelecidos cerca de 1000 resultados de Cálculo Infinitesimal.

o        De modo bastante simplificado, podemos dizer que:

§     Leibniz , em 1684, iniciou essencialmente o Cálculo Diferencial. Contudo, ao contrário do atual CD que é baseado na noção de derivada, o CD de Leibniz era baseado na noção de diferencial.

§  Newton foi o primeiro a usar sistemáticamente o Teorema Fundamental do Cálculo Integral , descoberto por Barrow, e demonstrou sua utilidade na descoberta de grande quantidade de resultados em Matemática e Física. Essas descobertas foram feitas entre 1666 e 1676, mas a maioria só foi publicada após 1700.  

Click aqui para ver exemplos e mais detalhes sobre as ideias de Leibniz e Newton.

4. O primeiro livro-texto de Cálculo Infinitesimal

Foi publicado em 1696 pelo Marquês de L’Hopital: Análise dos Infinitamente Pequenos.

É muito instrutivo observar os títulos dos capítulos desse livro:

Princípios do CI. Tangentes. Extremos. Inflexões. Envoltórias. Cáusticas. Evolutas. Ciclóides. Método de Descartes e Hudde.  

5.   Mas e antes dos europeus renascentistas?  

O CÁLCULO INFINITESIMAL COM PADRÃO CIENTÍFICO

  

1.     O concurso-desafio da Academia de Ciências de Berlin

Durante o século dos 1 700, o CI muito desenvolveu-se, principalmente através das descobertas de Euler. O próprio Euler escreveu um livro de Cálculo Infinitesimal que ainda hoje vale a pena ser lido.

Mas esse desenvolvimento muitas vezes apelava para argumentos mais baseados na intuição do que na razâo lógica, e não raramente produzia resultados errôneos. O padrão científico desse Cálculo ainda era baixo.

Procurando impor um padrão de trabalho mais rigoroso, a Academia de Berlin em 1786, em comissão presidida por Lagrange, anunciou um concurso-desafio à comunidade matemática: ganharia um valioso prêmio quem fosse capaz de criar um formalismo rigoroso para o Cálculo.

O ganhador foi um matemático francês chamado L’Huilier. O formalismo que ele desenvolveu introduzia formalmente a noção e notação de limite e é, essencialmente, o que hoje chama-se de Cálculo baseado em épsilons e deltas.

 

2.     Amadurecimento:

O formalismo de L’Huilier foi propagandizado e desenvolvido por Cauchy em seus cursos na Escola Politécnica de Paris e , por isso, a quase totalidade das pessoas acha que é a ele devido.

Outras componentes do Cálculo Moderno, como a noção de integral de Riemann e os resultados básicos sobre sequências, foram produzidos pelos matemáticos alemães do final do século passado ( Weiertrass, Dedekind, Bolzano, etc).

Como uma espécie de reação a essas idéias, que entre outras coisas pretendiam expulsar os infinitésimos de todas as áreas do Cálculo, Paul Du Bois Raymond desenvolveu, no final do século passado, um formalismo perfeitamente rigoroso para os infinitésimos. O autor desta página tem, modestamente, como fontes de inspiração e orientação justamente Du Bois Raymond e seu maior divulgador, J. Bertrand, bem como o nosso brasileiro Lélio da Gama. 

 

Fontepesquisa:(CARAÇA, BENTO J., 1951, Conceitos fundamentais da Matemática, Lisboa; http://euler.mat.ufrgs.br/~portosil/oque.html)

POSTED BY SELETINOF 10:39 PM   

NASA SELECTS TARGET CRATER FOR LUNAR IMPACT OF LCROSS SPACECRAFT

 

 

POSTED BY SELETINOF 8:58 AM